Discovery of the Hundred-Year-Old Lost Mathematical and Physical Relationship Between the Classical Kinetic Energy of Photons and Planck's Everlasting Experimental Equation in the Universe (Planck-Saleh Energy Equation)

Since a photon is emitted from an excited electron, and this electron has rotational motion around itself and the nucleus of an atom, the motion of the emitted photon must be a combination of linear projectile motion and the electron's rotational motions around itself and around the nucleus. The combination of linear motion and the rotation of electron around the nucleus creates a helical motion. When this is combined with the electron's self-rotation, a second helical motion is generated. Hence, a photon released from an electron has a nested helical motion. Initially, we will calculate the speed of the photon in this nested helical path and then use this speed to calculate the classical energy of the photon and its relation to Planck's everlasting energy equation.

1. Introduction

To show the hundred-year-old lost relation between classical energy and Planck’s energy, we first calculate the various speeds of the photon.

1.1 Calculation of the Linear Speed of Photon

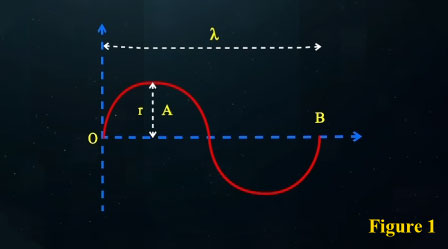
In these calculations, we find that if a photon traverses the straight distance between the points O and B (which is the same wavelength λ) in one period T, its speed equals:

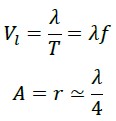
However, it has been experimentally proven that this value is indeed C.

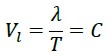
1.2 Calculation of the Wave Speed of Photon

If we consider the photon's motion along its curved path, we find that the distance travelled by the photon between points O and B exceeds λ. The actual distance travelled by the photon divided by the time taken T, gives us the photon's wave speed over one complete cycle.

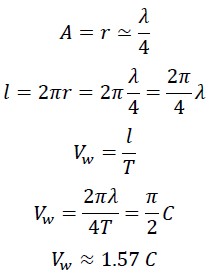
1.3 Calculation of the True Speed of Photon in the First Helix

In its first helical motion, the photon’s speed is the result of its linear speed and its wave speed, which are perpendicular to each other. Therefore, the true speed can be calculated using the following equation:

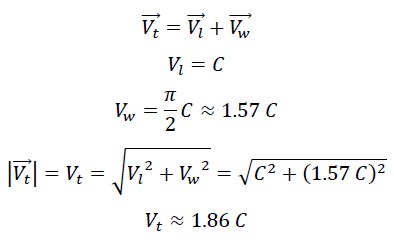
1.4 Calculation of the Speed of Photon in the Nested Helix

The motion in the nested helix results from the combination of two wave motions and one linear motion. The two wave motions are aligned and perpendicular to the linear motion, so the total speed is:

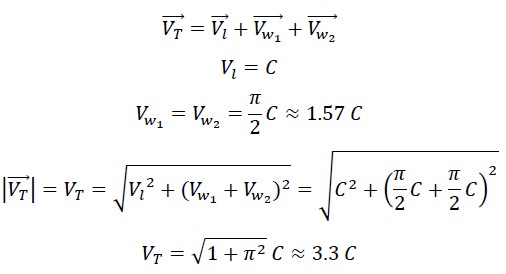
2. Calculation of the Classical Kinetic Energy of Photons

In this part, we calculate the energy of photon considering its helical motion:

initial total kinetic energy = linear energy + rotational energy = Translational energy + rotational energy

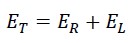
Where E_T is the initial kinetic energy, which is always constant and equals half the mass of the photon m_p times the square of the nested helical speed V_T:

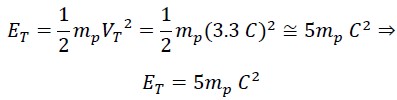
This energy consists of two parts: rotational energy of photon E_R which depends on the constant angular velocity and the variable rotational radius:

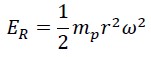
The second part is the translational (linear) energy, which equals the same energy measured by Planck in the laboratory, i.e., Planck’s constant times the frequency:

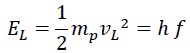
The sum of rotational and translational energy is always constant and equals the total energy, so the following equations can be written:

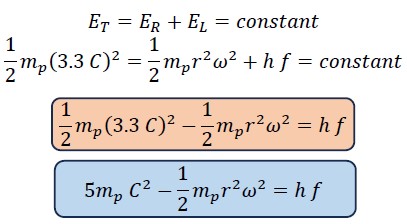
Now, we divide the first equation by the constant E_T

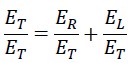
We define the two variable parameters as follows:

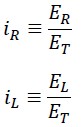
The following result can be derived from the above equations:

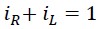
In other words, each of the translational energy E_L and rotational energy E_R be considered as a fraction of the total energy E_T

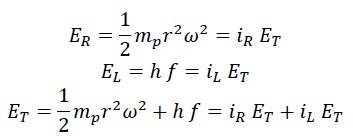
Since the total energy E_T is always constant, it can be understood that as the rotational radius r increases, the rotational energy increases and the translational energy decreases, resulting in a decrease in frequency f, and vice versa. As the rotational radius r decreases, the rotational energy decreases and the translational energy increases, increasing in frequency f.

Thus, the following graphs of the variations in translational energy E_L and rotational energy E_R relative to the rotational radius r can be drawn:

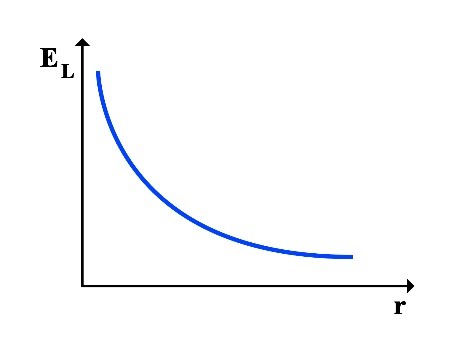
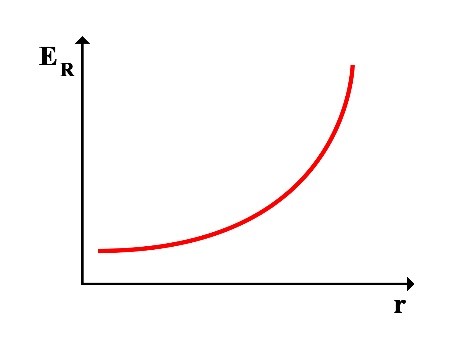
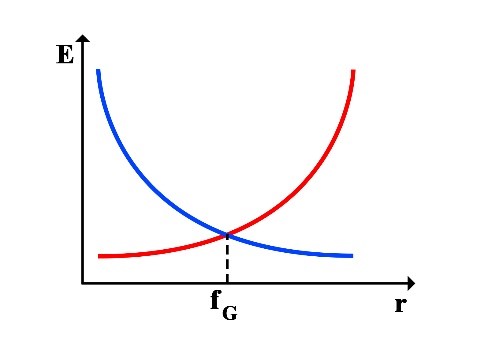
2.1 Calculation of Frequency at the Point of Equality between Translational and Rotational Energy

Now, we calculate the frequency at which the translational energy E_L and rotational energy E_R of the photon are equal:

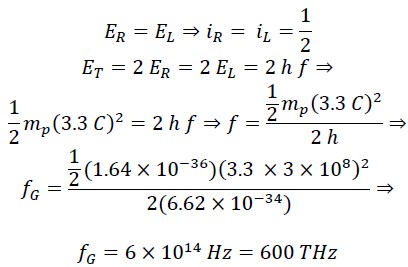
This frequency f_G corresponds to green light in the visible spectrum. At this frequency, the rotational energy equals the translational energy, and i_R = i_L = 1/2. Considering the frequency range of visible light, it can be said that in the frequency range of 300 THz to 900 THz, the range of 𝑖_𝑅 𝑎𝑛𝑑 𝑖_𝐿 will be as follows:

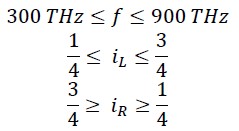
In fact, the relationship between i_L and f (Terahertz) can be written as follows:

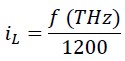
2.2 Relationship between Planck's Energy Equation and Classical Kinetic Energy (Planck-Saleh Energy Equation)

From the equivalence of translational energy with Planck's energy equation, we can write:

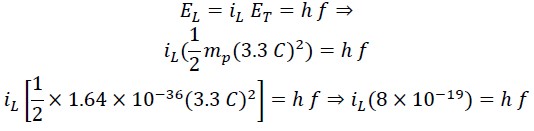
We call the constant value the Saleh constant "S" and rewrite the above equation as follows:

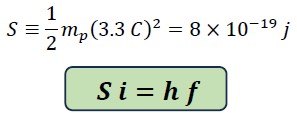
This equation is called the Planck-Saleh equation, where S is the Saleh energy constant and i is a variable coefficient equal to i of L and indicates the variations in translational energy.