Light Speed Barrier Broken!

Merely looking at the world around us, let us discover that, at the microscopic or macroscopic level, the rotational movement is more remarkable than the other types of movement existing in the Universe. For example, if we observe the electron well, we notice two rotational movements: around itself, and around the core. As far the moon, it turns around itself, around the Earth which rotate about its axis, and also around the Sun. The Sun itself, at the same time, revolves around itself, and around the galactic center. Even our galaxy, the Milky Way, follows the same rule and is simultaneously rotating around itself and around the supposed center of the Universe. Now we are going to study the speed of the astronomical objects at the hypothetical edges of the Universe:

Method A

Let us use the basic formula of speed equal to the distance divided by time and suppose that the orbit is a circle centered on the assumed center of the Universe. Then, knowing the period and the radius of rotation, we can calculate the average orbital speed for each of these celestial objects. The rotation period of the Moon is about one month or 0.08 year and the rotation radius is about the 10⁵ km. That being said, the speed is around 10³ km/h. As the radius increases, the speed increases. Two important points can be noticed in this table: first, the further away an object is from the center of rotation, the higher the speed gets. Second, the rotation period of celestial objects is much shorter than their lifetime.

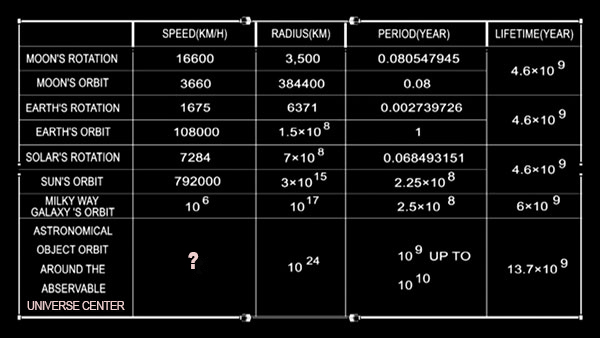
To complete this table, we need the measure of the observable Universe. The most recent research recognizes the most distant celestial objects at 10²⁴ km. Since the age of our Universe is estimated at about 13.7 billion years, to measure the speed of a celestial object rotating at the edges of the observable Universe, we take the rotation period between 1 and 10 billion years. By a simple calculation, we can see that the speed at the edges of the Universe is approximately between 10¹¹ or 10¹² km/h that is 100 or 1000 of times greater than the light speed which is about 10⁹ km/h in vacuum.

Method B

The cosmological principle posits the following: Viewed on a sufficiently large scale, the properties of the universe are the same for all observers and according to the Copernicus principle; the universe is globally homogeneous and isotropic. In such a system, the sizes do not change suddenly and from one corner to the other, some harmony could be observed. Suppose a celestial object rotates at a different angular velocity. According to Newtonian laws, this object must pass into another orbit and it is even possible that it strikes another object and consequently disrupts the homogeneity of the Universe. So we can say that all celestial objects revolve around the supposed center of the Universe at different distances but with an identical angular velocity and it is this identity that causes the homogeneity of the Universe on large scales.

For example, if we observe the radius of the orbit of satellites as well as their average speed, we can notice that the fastest, are those that turn further away from the Earth to be able to remain in an orbit with a fixed radius. Thus the value of the speed divided by the radius of rotation, i.e. the angular velocity, remains invariable. We know that the speed of the moon around the Earth is 3600 km/h. And that the Earth's speed around the Sun is 108,000 km/h. As far the celestial objects, which are at the edges of the Milky Way, at 10¹⁷ km from its center, it reaches a speed of 10⁶ km/h. According to the latest research, the most distant celestial objects are at 10²⁴ km.

From the homogeneity of the Universe, we deduce the identity of the angular velocity everywhere in the Space and we can, therefore, say that the angular velocity at the edges of the Milky Way and at the edges of the observable Universe is equal. If ω₁ and ϑ₁ would be the different speed values for celestial objects at the edges of the Milky Way and ω₂ and ϑ₂ would be the speed at the edges of the Universe, we can see that ϑ₂ is at 10¹³ km/h. Thus, this is 10 thousand times faster than light speed. By this calculation, we can prove that even celestial objects that are at 10²⁰ km rotate at the speed of light. Based on the cosmological principle and with simple calculations on the orbital speed and distance of the celestial objects, we can prove that any celestial objects located at 10²⁰ km up to 10²⁴ km are rotating with a speed of 10⁹ km/h.

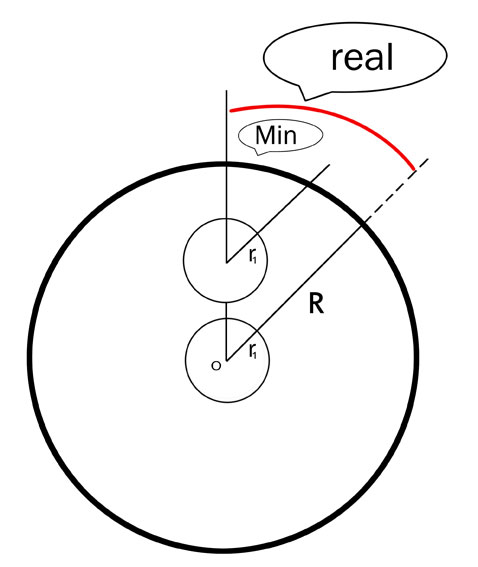
On the other hand, we know that the Milky Way is not at the center of the Universe and it is not adequate to compare the speed and the radius of rotation of the objects that rotate at the edges with those that rotate at the edges of the Universe. The more adequate comparison is about the length of the arc of the circle centered in O and radius r₁ with the length of the arc concerned on the circle of radius R. Taking into account the proportionality already mentioned, we can say that the calculated speed is, in fact, the minimum possible speed of the rotation of objects at the edges of the observable Universe. And certainly, billions of celestial objects are currently rotating at the edges of the Universe at a speed that is thousands of times faster than light speed.

Method C

10²⁴ km is the radius of the observable Universe; this means that science is unable to go further. Let us assume that the real value of the Universe radius would be 10⁵⁰ km. By a simple calculation we could find out that the speed of celestial objects at the edges of the Universe is billions of times greater than that of light.

Thus, millions, billions and millions of billions of objects are currently rotating with a speed thousands of times greater than that of light!