
New Calculation of the Angular Velocity and Rotational Radius of Photons in the Universe
In previous articles, we calculated the rotational and translational energy of photons using the speed of photons in a nested helical path (VT = 3.3 C) and we examined its relationship with Planck's energy equation. We now proceed to calculate the constant angular velocity (ω) by equating the translational and rotational energy at a frequency of 600 THz. Subsequently, considering the constancy of the angular velocity across all frequencies, we derive a formula to calculate the radius of the rotation of photons (r) in terms of the variable coefficient of rotational energy (iR). Finally, we calculate the rotational radius for several frequencies within the range of visible light.
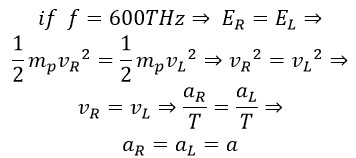
Where aR is the amplitude of rotational motion and aL is the amplitude in linear motion. The rotational radius is the vector sum of these two perpendicular quantities. Therefore, we have:
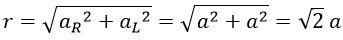
At a frequency of 600 THz, the linear amplitude is one-quarter of the wavelength, so we have:
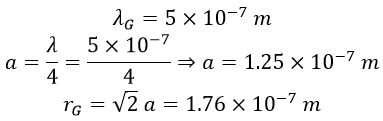
Now, with the rotational radius for green light at a frequency of 600 THz, we calculate the constant angular velocity of photons:
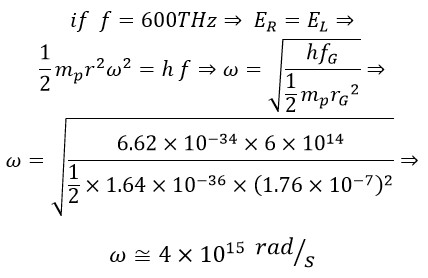
Using the obtained angular velocity, for the rotational radius of photons, we have:
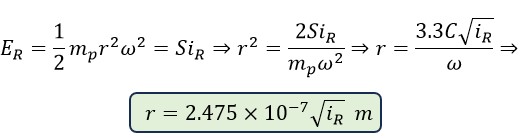
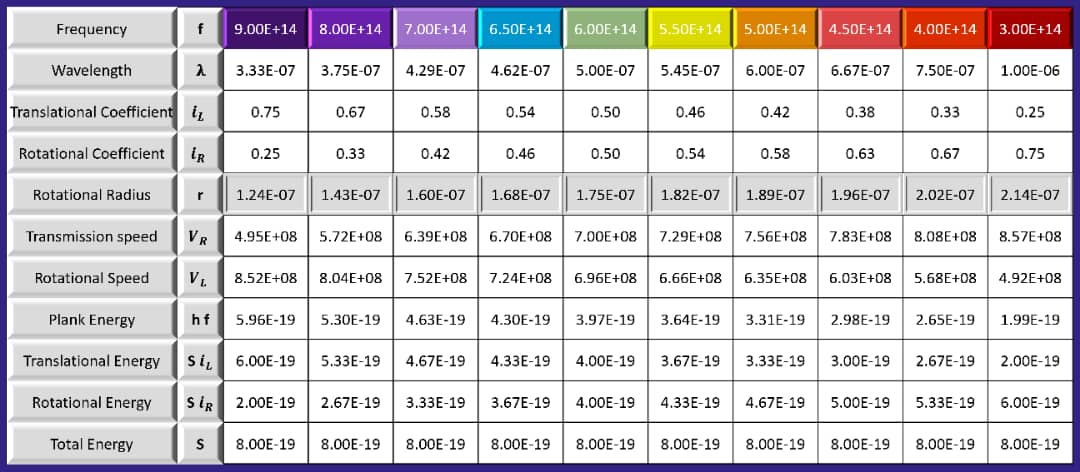
Now, by substituting different values, we obtain the rotational radius of several visible light spectra:
Finally, we calculate the linear and rotational velocity for the frequency f = 600 THz, where ER =EL, using two methods and comparing the results.
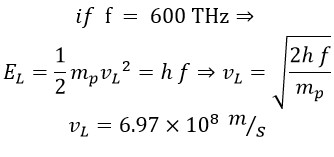
On the other hand, for the rotational speed, considering the rotational radius rG = 1.76 × 10-7 and ω = 4 × 1015 so:
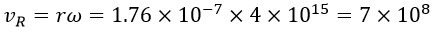
By comparing the obtained rotational and linear speeds, it is evident that both values are equal, which serves as proof of the accuracy of the presented calculations.
Articles




