New Discoveries About the Nature of Black Holes and Their Structural Model 2025

If we consider the atomic model of elements, which includes a central nucleus and electrons orbiting around it, we can observe that the model and density of each element will differ from other elements. This occurs because in atomic nuclei, the number of protons (along with neutrons) increases with changes in atomic number, and the electrons that orbit the nucleus also increase following the increase in protons. In essence, alterations in these particles lead to changes in density, meaning different elements possess different densities. Indeed, density can be used as a factor for comparing elements.

If we wish to define a model and nature for black holes, we must consider their density, which is approximately between 10²⁰ and 10³² kg⁄m³. Upon investigating which particle could generate such a density within this range, we examine the following:

However, as the densities of these particles are less than that of black holes, they certainly cannot produce the requisite density for a black hole.

For a better understanding, let us turn our attention to white dwarfs and their constituent unit, the proton. Consider white dwarfs, which are formed after a stellar explosion and have a density about 10⁹ kg⁄m³. This density, being less than that of a proton, allows for the possibility that white dwarfs are composed of protons.

It is abundantly clear that these particles (photons, electrons, and protons) do not possess the capability to create the density required for black holes. Therefore, we must define a particle that can create this density – a particle smaller than a photon.

Just as an atom has a structure, and a solar system has a structure, a photon also has a structure that can be broken down into smaller constituent particles. These particles would assuredly have a higher density than the photon itself. One of the particles proposed by the Saleh Research Group is a subatomic particle named "Cidtonium-1". This particle could have a density up to 10⁶ times that of a photon.

In reality, the proposed Cidtonium-1 would have a density of approximately 10²⁰ kg⁄m3. However, as we have demonstrated in previous articles, the density of black holes ranges from approximately 10²⁰ to 10³² kg⁄m³. Consequently, only a certain subset of black holes could be composed of the Cidtonium-1. We can, therefore, conclude that to form different black holes with their specific densities, "sub-Cidtonium-1" particles must also exist.

We shall call the first of these "Cidtonium-2", which could have a density 10⁶ times that of Cidtonium-1. The subsequent particle would have a density 10⁶ times that of Cidtonium-2. So:

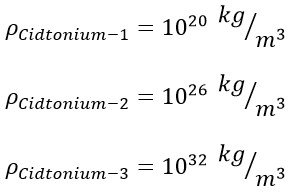
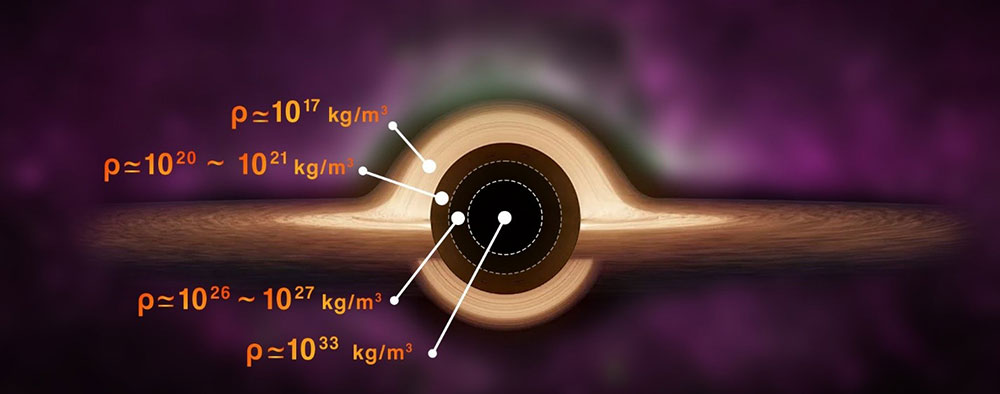
Thus, we can define three models of Cidtonium to account for the density of a supermassive black hole. It can be stated that as the density of the particles increases, their sub-photon structures will also change. Based on this, the general form of a large black hole with a density of around 10³² kg⁄m³ can be demonstrated as follows.

References:

[1] Saleh, Gh. "A New Explanation for the Creation of Black Holes, White Dwarfs and Magnetars." Frontiers in Cosmology and Gravitational Physics 2024 (2024): E2.

[2] Saleh, Gh. "A New Explanation for Black Holes and White Holes." Saleh Theory, 24 Apr. 2023, https://www.saleh-theory.com/article/a-new-explanation-for-black-holes-and-white-holes

[3] Saleh, Gh. "New Explanation for Why Black Holes Are Invisible." APS Northwest Section Meeting Abstracts. Vol. 23. 2023.

[4] Saleh, Gh. "New explanation about the structure of black holes." International Annual Meeting of the German Astronomical Society (AG meeting 2023. 2023.

[5] Saleh, Gh. "A New Explanation for How Black Holes Are Created and Their Types." The 54th Conference of the European Group on Atomic Systems (EGAS 54. 2023.

[6] Saleh, Gh. "The outward/inward nature of black holes and their structure (beyond the standard model)." 14th Conference on the Intersections of Particle and Nuclear Physics (CIPANP 2022. 2022.

[7] Saleh, Gh. "The New Structure for Black Holes and their Nature." APS Southeastern Section Meeting Abstracts. Vol. 89. 2022.

[8] Saleh, Gh. "The outward/inward nature of black holes and their structure (beyond the standard model)." 14th Conference on the Intersections of Particle and Nuclear Physics (CIPANP 2022. 2022.

[9] Saleh, Gh. "The New Structure for Black Holes and their Nature." APS Southeastern Section Meeting Abstracts. Vol. 89. 2022.

[10] Saleh, Gh, M. J. Faraji, and R. Hashemizadeh. "Explanation of the nature of black hole and its possible creation ways." APS Meeting Abstracts. 2021.