
New Discoveries About the Speed of Electromagnetic Waves 2024 Part C
To explain the broadening phenomenon and the results of MIT and University of Michigan experiments, one should first explain the helical motion principle and calculate its velocity in the universe:
a) New Explanation and Calculation for the First Helix, Second Helix, and Third Helix Motion Paths and Their Speed
b) New Explanation for the Broadening Effect in Electromagnetic Waves
c) New Explanation for the Experiments of MIT and University of Michigan; Breakdown of the Planck's Law at Nanoscale Gaps
a) New Explanation and Calculation for the First Helix, Second Helix, and Third Helix Motion Paths and Their Speed
Considering that the birthplace of a photon is an excited electron that rotates around a nucleus and the excitation of an electron results in the emission of a photon, the photon will have linear motion. The linear speed of the photon Vl can be calculated using the following equations:
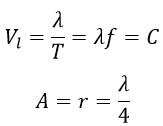
The above equations are linear equations in which “λ” represents the wavelength, “T” the period, “f” the frequency, and “A” the amplitude, which is equal to the radius of photon rotation in a helical motion (r). These equations express linear speed and are obtained by dividing the linear distance traveled (λ) by the time taken during one period (T). In fact, we have calculated the linear speed along the linear path.
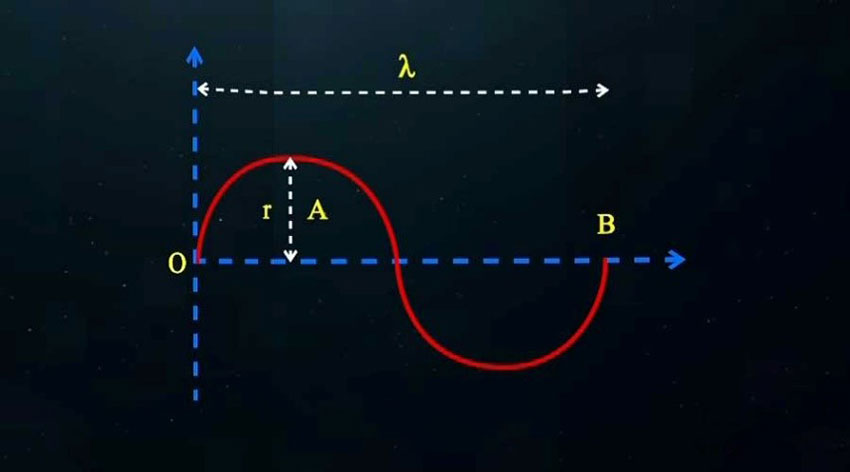
However, a photon has a wave motion due to the rotational movement of electrons around the nucleus. To calculate the wave path or the curved path of electromagnetic waves, we proceed as follows:
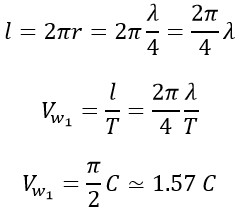
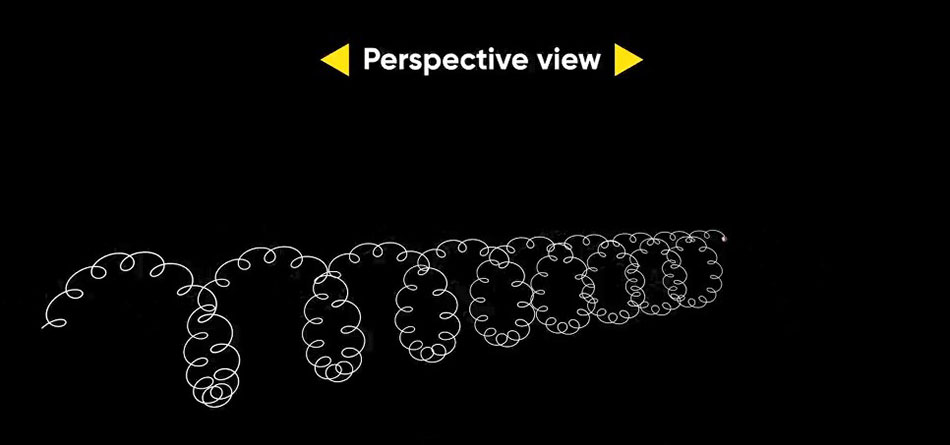
Where “l” is the traveled distance and (Vw1 is the wave-like speed. The result of combining these two linear and rotational motions is the creation of a helical motion as shown in the following figure.
If we pay attention, a photon has two different speeds. This difference exists both in terms of the appearance of equations and the ones of obtained values. In fact, these two speeds (linear and wave-like) can be considered as shades of the speed in helical motion. Where (Cnew 1 is the constant speed on the helical path, which is the resultant of these two perpendicular velocities. which can be calculated as follows:
Resultant velocity = Linear velocity = Wave-like velocity
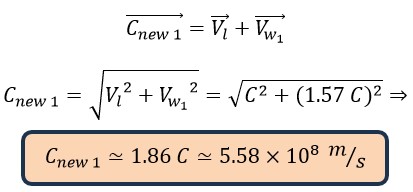
Where the (Cnew 1 is the speed of the photon in the large helix (First Helix) which is the basic and fundamental speed of photon (electromagnetic waves).
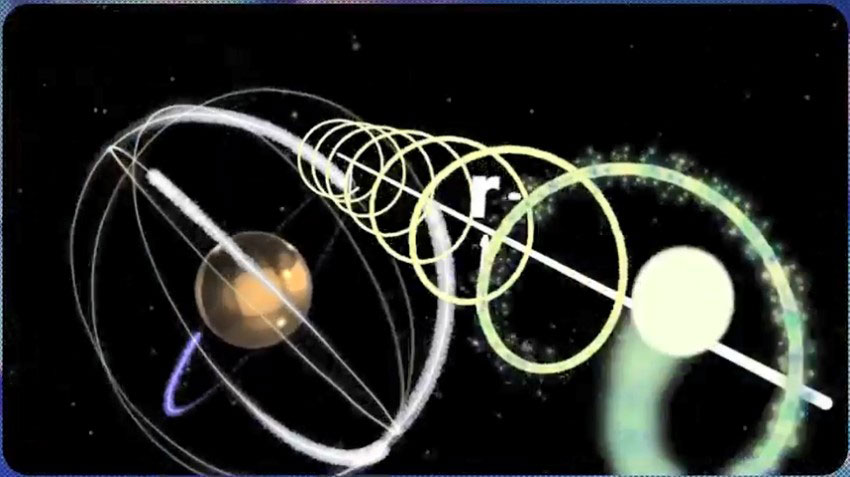
But an electron, in addition to its rotational motion around the central nucleus of the atom, also has rotational motion around itself, leading to the creation of another helical motion. This new helix (Second Helix) is smaller in comparison to the previous one. Therefore, when a photon is emitted from an electron, it will follow a path of a large helical motion (First Helix) and a path of a smaller helical motion (Second Helix).
Considering the above figure, the resultant velocity of photon in the first helix and second helix motion paths can be calculated as follows:
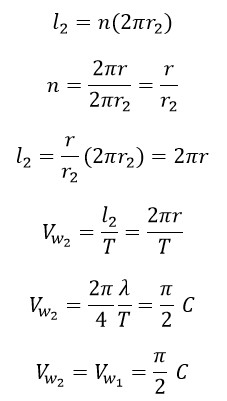
Where “l2” is the traveled distance in small helix, “n” is the number of turns of photon in small helix in one period of big helix, “r2” is the radius of small helix and “Vw2” is the rotational speed in small helix. And two rotational velocities are parallel. So, we have:
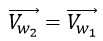
Considering the figure, the resultant velocity of a photon (Cnew 2) in two helical paths, the large helix (first) and the small helix (second), can be obtained from the following equations:
The resultant velocity = The sum of the velocities in the two helical paths + The linear velocity

The photon itself also has a rotational motion around itself, which creates a third helix. Using the following equations, this speed can be calculated:
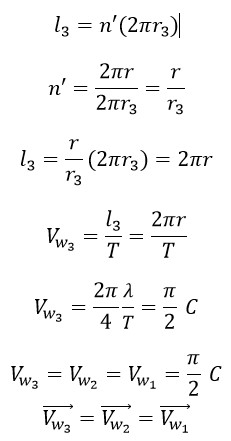
Where “l3” is the traveled distance in third helix, “ n' ” is the number of turns of photon in third helix in one period of big helix (first), “r3” is the radius of third helix and “Vw3” is the rotational speed in third helix.
Similarly, the resultant velocity of a photon (Cnew 3) is equal to the sum of its speed in helical paths and the linear speed. Therefore, we have:

In light of the calculation method where rotational speeds are summed, and their result is added to the linear speed, the following relations can be written for the resultant speed of photon (Cnew m) in “m” helix:

Notice 1:
All the speeds obtained are a constant coefficient of “C”. Therefore, all the obtained speeds are also constant.
b) New Explanation for the Broadening Effect in Electromagnetic Waves
As mentioned in part “a”, photon (electromagnetic waves) has nested helical paths, as shown in figures.
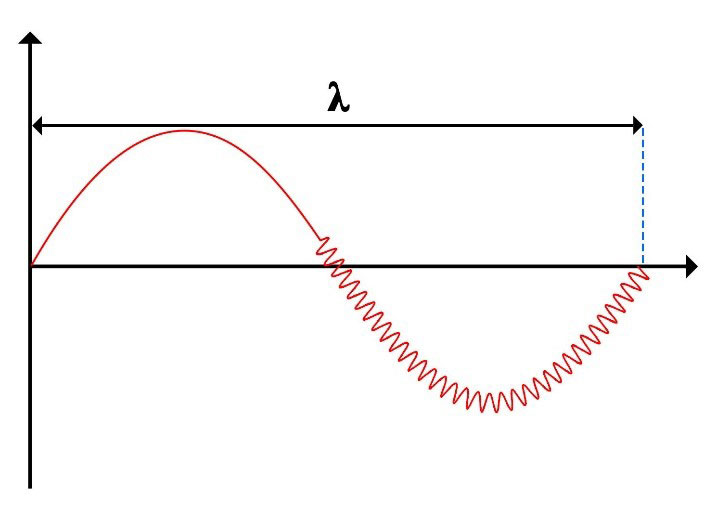
Left part of the above figure depicts the path of a simple photon (electromagnetic wave) with no additional effects. However, right part illustrates a nested helical path, resulting from the combination of two different paths, a larger helix and a smaller one. In essence, the second helix (small) broadens the first helix (large). This phenomenon observed in various experiments is called the “Broadening Effect”.
c) New Explanation for the Experiments of MIT and University of Michigan; Breakdown of the Planck's Law at Nanoscale Gaps
Max Planck presented his law in 1900 regarding the relationship between energy and wavelength. This law states that radiation associated with different wavelengths has a linear relationship with energy. However, researchers from the Massachusetts Institute of Technology (MIT) and the University of Michigan have demonstrated that this law holds only at long distances and large scales, and it is violated at short distances [1, 2]. This experiment was conducted by MIT researchers and has recently been repeated by researchers at the University of Michigan. They used a very small metal and glass surface, and an atomic force microscope with high precision to measure thermal changes exchanged between these two objects. As a result, they found that at a 10-nanometer distance, thermal conduction can be up to 100 times greater than the predictions of Planck's law. However, an explanation for this phenomenon has not been provided. This section elaborates on this topic, taking into account the information presented in part “a”, where the photon's path is a nested helical path, and considering 3 nested helixes (that is real and actual in the ideal state), we delve into the examination of photons in the early moments of emitting from electron.
In accordance with Saleh Theory, the mass of photons is a constant value (m = 2.6 × 10-36 kg), like their speed (C), therefore, the product of half of the mass and the square of the speed (1/2 mv2), which is the initial kinetic energy of a photon at the time of t=0, is a constant value. At t=0, this energy is equal for all electromagnetic wave spectra. However, due to the difference in the radius of rotation in the helical path in different spectra, the rotational energy they consume varies (1/2 mr2 ω2). Hence, the translational energy of photons, which is the same as the value obtained in Planck's law (hϑ), is specific and different for each spectrum with different frequencies.
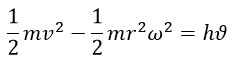
In fact, it can be said that although different energy values are considered for photons with different frequencies, at t=0 or t=ε the energy value of all of them is equal because there is no rotational motion at that time.
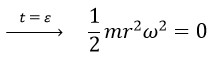
So, we can use the final speed of photons, which is the speed with the presence of 3 nested helixes (v=Cnew 3), to calculate the initial energy:
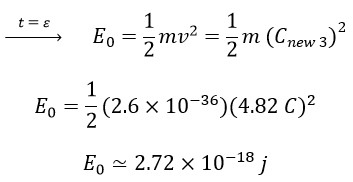
Now, let's calculate the energy for the infrared spectrum (ϑ = 4.5 × 1013Hz) using Planck's law:
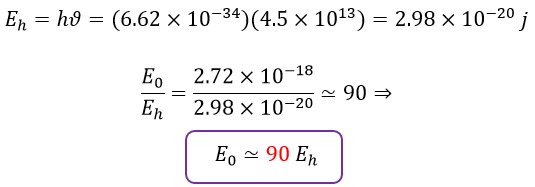
Considering the two energy values, the initial energy (E0) and the frequency-dependent energy predicted by Planck's law (Eh), it can be said that the energy obtained in the early times or short intervals after the emission of photons is almost 90 times the energy obtained from Max Planck's law, and most of the energy of the emitted photon from its associated electron is consumed in the helical motion.
On the other hand, as previously explained, physicists at the University of Michigan demonstrated a violation of Max Planck's law in the case of short distances in the laboratory [1, 2]. They have shown that the translational energy at very short distances (less than 10 nanometers) can be more than 100 times greater than the energy predicted by Planck's law. In fact, it can be said that the experiments conducted at MIT and the University of Michigan are acceptable by using these explanations. And this a confirmation of the validity of the University of Michigan's experiment and the calculations of the Saleh Research Group. In other words, the explanations in this article confirm the experiment and the experiment confirms the explanations.
Notice 2:
In the calculation of the ratio of the initial kinetic energy of a photon to the experimental Max Planck energy, all parameters are constant, and the main variable is only the frequency. Since the frequency in electromagnetic waves has a very wide range, this ratio will have significant variations. But in some ranges, the result shows a number greater than reality.
Given that the experiment of dear Max Planck was performed in the visible light range, for example, the ratio of the initial kinetic energy to the translational energy (Max Planck energy) for 3 specific frequencies in the red, green, and violet spectra is calculated:

The values obtained for the energy ratio in the visible light range are between 5 and 10. It can be said that in the frequency range of visible light spectrums, the value of the ratio of the initial kinetic energy of a photon (E0) to the Max Planck energy (Eh) has a range between 5 to 10, or the Max Planck energy value is 1/10 to 1/5 of the main (initial) energy value.
Notice 3:
If we use the speed (Cnew 1 ≃ 5.58 × 108 m⁄s) instead of the speed (Cnew 3 ≃ 1.446 × 109 m⁄s) in calculating the initial energy, the result of the calculations becomes in a way that the energy ratio in the visible spectrum range becomes about "0.8":
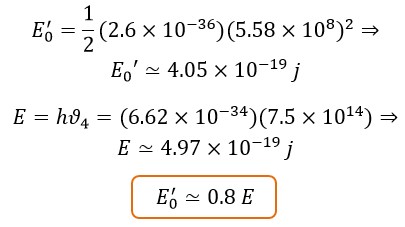
This means the translational energy of Max Planck (E) is greater than the initial energy (E0'), which is contradictory and impossible. Therefore, the existence and use of the speed “Cnew 3” or “Cnew 2” is logical and correct.
Reference:
[1] Chandler, David L. “Breaking the Law, at the Nanoscale.” MIT News | Massachusetts Institute of Technology, news.mit.edu/2009/heat-0729. Accessed 29 July 2009.
[2] Thompson, Dakotah, et al. " Hundred-fold enhancement in far-field radiative heat transfer over the blackbody limit." Nature 561.7722 (2018): 216-221.




