Utilizing a simple lens, we choose filters at will (red, yellow, green, blue, and violet). Then, we apply the filter to the lens and locate a thermometer at its focal point. It is evident that the temperature shown on the thermometer is lowest when using the red filter, highest with the violet filter, and the green filter falls in the middle.
These results confirm the validity of Planck's universally accepted equation.
Despite our common perception of red light as warm and blue light as cool, the experimental data clearly demonstrate the opposite.
Next, we evaluate the results of two experiments conducted by physicists at the University of Michigan and the Massachusetts Institute of Technology [1,2]. These experiments indicate that Planck's equation does not hold at a very small scale from the light source. The main reason for this is that at very close distances to the source (d=ε or equivalently at t = ε), the amount of energy significantly exceeds the amount of energy that Max Planck predicted. This is because photons exhibit both linear and rotational motions. In the experiments conducted by the University of Michigan and MIT, the total energy was measured, whereas in Planck's experiment, only the linear energy was measured, not the rotational energy. The discrepancy in energy measurements (between the two university experiments and Planck's experiment) indicates the presence of rotational motion of photons or missing rotational energy [3].
Now, let's discuss the first question: why does red light appear warmer and blue light cooler?
A New Explanation for Why the Translational Energy (Derived From Planck’s Equation and Saleh’s Experiment) of Blue Spectrum Is Greater Than That of Red One, While Our Sense of Sight and Touch Perceive Red Light as Warmer, Larger, and Stronger Than Blue Light
Given that the photon traverses in a helical path; it has both linear and rotational motion, the energy of the linear motion (translational energy) can be easily calculated using Planck's equation and Saleh's experiment. Also, as the frequency of blue light is higher than that of red light, all measuring devices demonstrate the energy of blue light is greater than that of red light based on its frequency. When we observe a wave with a helical motion coming towards us from the front, such as the blue and red spectrum, it's clear that because the frequency of blue light is higher, its wavelength, amplitude, and rotational radius (rm) are smaller than those of red spectrum. Thus, the cross-section area of the blue spectrum is smaller than that of the red one. Consequently, red light stimulates a larger area on the retina or skin, activating more visual and tactile cells, and is perceived as stronger and warmer.
The internal energy of the red spectrum is greater than that of the blue one, and the translational energy of the red spectrum is less than that of the blue.
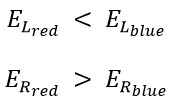
Overall, we perceive blue light as cold because, although the amount of its translational energy is greater, its rotational energy is less than that of red light. Conversely, we perceive red light as warm because, despite having less translational energy compared to blue light, it possesses greater rotational energy.
Notice:The speed of a photon has been considered to be "C", the energy of each photon was considered to be E=mpC2 and the classical energy of the photon was E = 1⁄2 mpC2. Where mp is the mass of the photon ( 𝑚𝑝 = 1.64 × 10−36𝑘𝑔). Recent calculations have shown that the speed of a photon is "3.3 C" [4]. Consequently, in the calculation of the photon's kinetic energy, the speed should be considered as v=3.3C. If the new speed is squared, which is 3.3 times the previous speed, the new energy value is approximately 10 times the previous energy. In other words, the new energy value has increased by a factor of 10 compared to the old one, or approximately 1000%, which corresponds to the value obtained in the MIT University experiment at a very small scale from the light source. Hence, the results obtained from the MIT University experiment are also correct and valid.
To enhance comprehension, we will calculate the different energies (translational, rotational, and total) of the end of violet light with a frequency of f=900 THz.
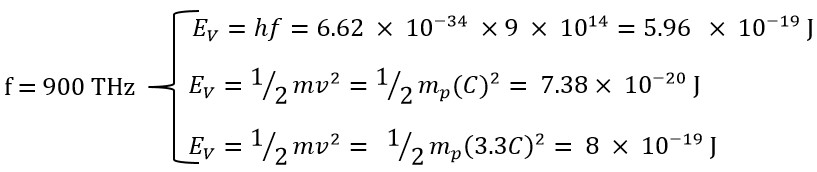
In this example, we used a frequency of 900 THz, for which the energy obtained using Planck's method is at its maximum (within the range of 300 to 900 THz) and its value is as follows:
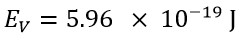
The obtained classical energy value, using the speed value of v=C, is equals:
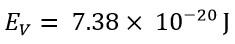
These two values show a significant difference. However, the classical energy value, using a speed that is v=3.3C, would be:
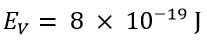
If we look at the obtained values, we will demonstrate that the photon's energy at a speed of v=3.3C is very close to the experimentally calculated energy by that of Planck, with a slight difference due to the rotational energy of the photon, which is not measurable in Planck's experimental method. Consequently, the rotational energy of the photon is not accounted for in Planck's relation.
Therefore, it can be stated that the value of the translational energy of a photon equals the established empirical value by Max Planck, which is valid. On the other hand, the energy value obtained from the MIT experiment and Saleh Theory calculations represents the total energy of the photon, and these two are also accurate, real, and acceptable.
In other words, the MIT University experiment demonstrates the total energy value. The empirical energy calculation method of Max Planck indicates the translational energy value, while Saleh Research Group's calculations show the values of translational, rotational, and total energy.
In previous articles, it was stated that the translational energy (EL) is a fraction of the total energy (ET), and this fraction for a electromagnetic wave with a frequency of f=900 THz equals iL = 3/4 [5]. In other words, its translational energy constitutes 75% of the total energy, while the remaining 25% is attributed to its rotational energy.
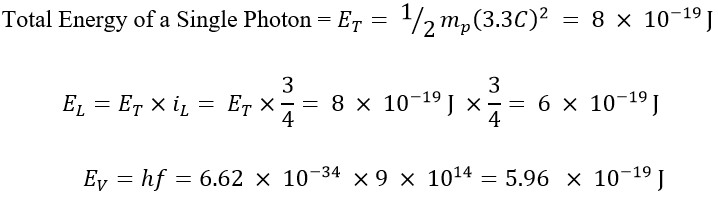
As evidenced by the observations, the value obtained for translational energy matches the energy obtained from the Planck method.
References:[1] Chandler, David L. “Breaking the Law, at the Nanoscale.” MIT News | Massachusetts Institute of Technology, news.mit.edu/2009/heat-0729 . Accessed 29 July 2009.
[2] Thompson, Dakotah, et al. " Hundred-fold enhancement in far-field radiative heat transfer over the blackbody limit." Nature 561.7722 (2018): 216-221.
[3] Saleh, Gh. "New Discoveries About the Speed of Electromagnetic Waves 2024 Part C." Saleh Theory, 06 Nov. 2023, https://www.saleh-theory.com/article/new-discoveries-about-the-speed-of-electromagnetic-waves-2024-part-c
[4] Saleh, Gh. "New Discoveries About the Speed of Electromagnetic Waves 2024 Part B." Saleh Theory, 30 Oct. 2023, https://www.saleh-theory.com/article/new-discoveries-about-the-speed-of-electromagnetic-waves-2024-part-b
[5] Saleh, Gh. "Discovery of the Hundred-Year-Old Lost Mathematical and Physical Relationship Between the Classical Kinetic Energy of Photons and Planck's Everlasting Experimental Equation in the Universe (Planck-Saleh Energy Equation)" Saleh Theory, 28 Jun. 2024, https://www.saleh-theory.com/article/discovery-of-the-hundred-year-old-lost-mathematical-and-physical-relationship-between-the-classical-kinetic-energy-of-photons-and-plancks-everlasting-experimental-equation-in-the-universe-planck-saleh-energy-equation
In this paper we introduce a equation which is called the Planck-Saleh equation, where 𝑺 is the Saleh energy constant and 𝒊 is a variable coefficient and indicates the variations in translational energy. This equation shows the relationship between Planck's Energy equation and classical Kinetic Energy