
Proof of the Rotation of the Nuclei of Atoms Using the Law of Conservation of Energy and Momentum
Method 1
Due to what was noted in previous articles including proof of emission of photons from electrons and the formation of protons and electrons from photons, the following relations can be written:
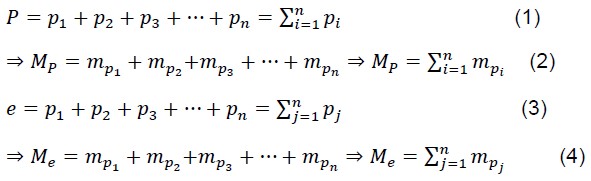
Where ,𝑀𝑃, 𝑚𝑝 𝑎𝑛𝑑 𝑀𝑒 are the mass of proton, photon and electron. Now we calculate the energy of each side of (1):
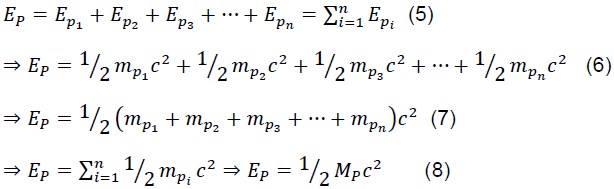
According to the equation, It can be concluded that based on the law of conservation of energy; the amount of energy of a proton is equal to the mass of it multiplies 𝐶2. It means that the nuclei of atoms that are the location of protons, rotates at the speed of light "C".
Method 2
If we impact a motionless mass and pieces detach from it, these detached pieces will fall next to the mass, but if we do with a rotating mass at high speed (for example, a piece of wood that is rotating at high speed), any piece that is separated from it will inevitably have a projectile motion. On the other hand, If we consider nuclear fission, in which the nucleus of an atom splits into two or more smaller nuclei, photons, etc., we can say that in the fission of a nucleus with a set of protons, we have:

So, it can be deduced that if the nuclei of the atoms have no motion, after impact, its remnants would fall next to it. But if the nuclei of the atoms have spins at high speed, any pieces that are separated from it would inevitably have a projectile motion.
In other words, in the nuclei of atoms, the separated particles, as a result of the explosion, can be thrown out with the speed of light "C" due to the high speed rotation of the nucleus. In fact the initial speed of all separated particles is caused by protons and neutrons that are inside the nucleus and are rotating at a speed of light "C".




