
New Discoveries about the Magnetic Fields
1. Calculation of Frequency and Energy of the Magnetic Fields
2. New Explanation for the Intense Attraction and Repulsion of the Magnetic Poles
3. Nature and Structure of Magnetic Fluxes
1. Calculation of Frequency and Energy of the Magnetic Fields
To calculate the frequency of the magnetic field, we use the following experiment: two annular magnets with identical characteristics are placed facing each other by the same poles. The upper magnet is in equilibrium thanks to the interactions between the force of its weight and the magnetic force of the lower magnet. Therefore, the gravitational potential energy of the upper magnet must be equal to the magnetic energy of the lower magnet. Then we measure the distance between the two magnets.
By multiplying this distance with the mass and the gravitational constant of the Earth (g=10) we obtain the gravitational potential energy of the upper magnet which is equal to the magnetic energy of the lower magnet. On the other hand, we consider the magnetic energy of the magnet as “nhϑ” and deal with the calculation of the frequency of the magnetic field of the magnet. So we have:
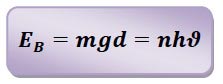
The above tests are repeated by different magnets.
Case 1: Both the lower and upper magnets are 2.5 grams:
The distance between the two magnets is 2.30 cm. Therefore we have:
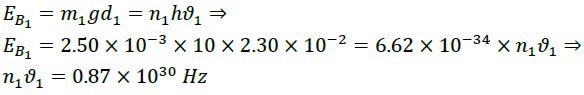
Case 2: Both the lower and upper magnets are 5 grams:
The distance between the two magnets is 2.32 cm. Therefore we have:
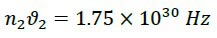
Case 3: Both the lower and upper magnets are 7.5 grams:
The distance between the two magnets is 2.33 cm. Therefore we have:
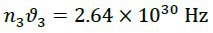
We continue the same approach and we have obtained the result that present in table 1.Based on the above experiment, it can be concluded that:
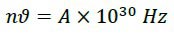
In which 1030 is our constant and there is a variable coefficient “A”
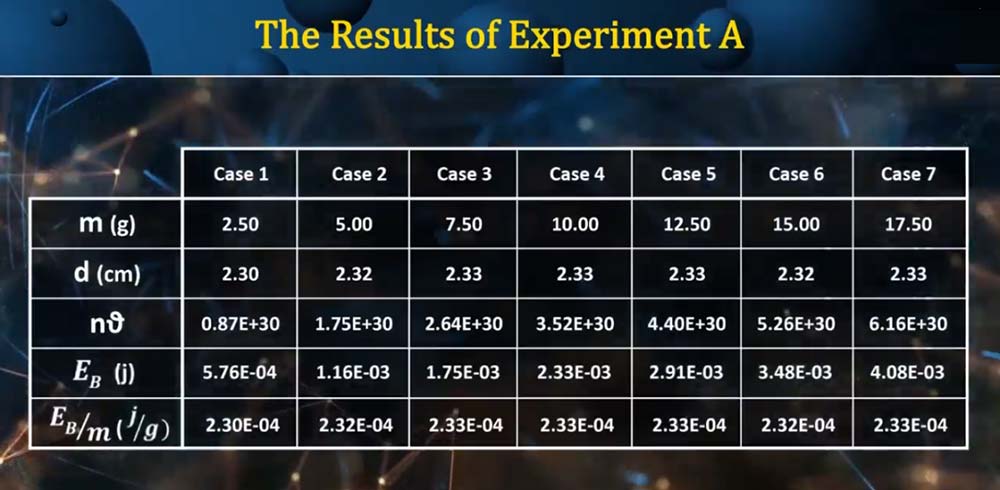
Table 1
Notice:
As we know, force lines or magnetic fluxes are invisible and on the other hand, they pass through objects. Considering these characteristics, we can certainly say that the frequencies of magnetic fluxes are obviously higher than those of visible waves. It can therefore be deduced that the start of the frequency range of the magnetic field must be 1015 Hz. So in this test the amount of "n" is also around 1015.
We repeat the experiment with 45 grams magnets and the following results is obtained (Table 2):
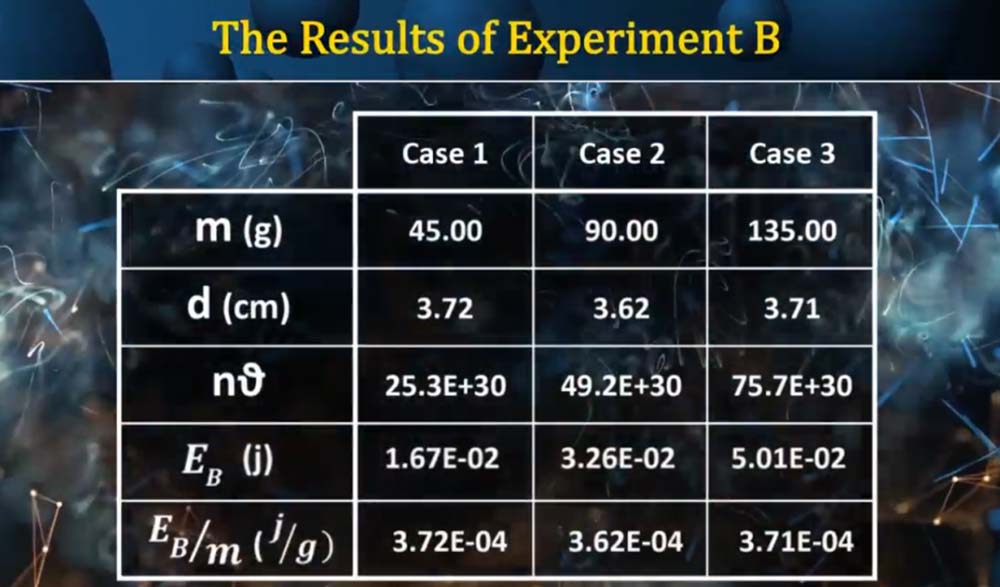
Table 2
In this experiment, we reach similar results. So, it can be said that logically the beginning of the frequency range of magnetic waves should be 1015 Hz, and therefore the beginning of the interval of "n" is 1015 too. On the other hand, as you can see, the value of distance “d” is between 2.30 and 3.72 cm. And according to the formula obtained for the magnetic energy of the magnet (𝐸𝐵 = 𝑚𝑔𝑑) and averaging the energies obtained in the experiments per gram of magnet, the energy of one gram of ordinary laboratory magnet can be considered approximately equal to 3×10−4 𝑗/𝑔. We call that as “Saleh Energy Constant” (𝑺𝒆).
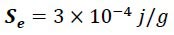
So the amount of magnetic energy of ordinary laboratory magnet is generally equal to:
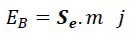
Where, “m” is mass in units of grams. Therefore, by measuring the mass of a magnet and using this formula, the energy of the magnet can be easily obtained.
Notice:
1- Considering that 𝑛𝜗 always has the constant part of 1030, by increasing the magnet mass, the coefficient 𝑛𝜗 will change and the value of 1030 always will be constant.
2- Although by increasing the mass of magnet, the number of magnetic fluxes “n” and magnetic field frequency will increase but this increase is such that the frequency remains in range of 1015 to 1016 Hz.
Now we will study the dependency of magnetic frequency ϑ and the number of magnetic fluxes “n” to the mass. As it was said before, the frequency will remain in the range of 1015 to 1016 Hz. So the number of magnetic fluxes can be defined as follow:
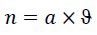
Where “a” is between "1" and "10", therefore:
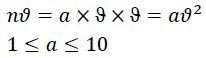
On the other hand, we obtained:
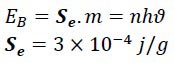
As a result:
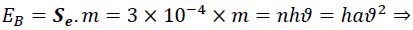
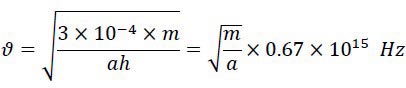
As we said before:
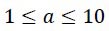
So:
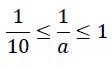
By averaging ⚊1𝑎 and putting it in the relation, we have:
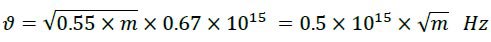
The constant value is called “Saleh Frequency Constant” (𝑺𝝑) and we have:
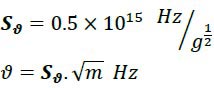
Where “m” is the mass of the magnet in units of grams.Therefore, by measuring the mass of the magnet and using this formula, the magnetic frequency of the magnet can be easily obtained. As a result, the energy and frequency of the magnets can be easily calculated by these two formulae


Notice:
1- It should be noted that as it was said previously, by increasing the magnetic mass, in addition to the frequency, the number of magnetic fluxes will increase accordingly. But considering the limitations of the frequency range of the magnetic field it can be concluded that although the magnetic frequency of magnets is dependent on mass, but it has limitations and always will be remained in an approximate range of 1015 to 1016 Hz (Fig. 1). But the magnetic field energy of magnets, considering the wide range of variations for n, may have lower limitations.
2- The accuracy of these formulae is about 97%.
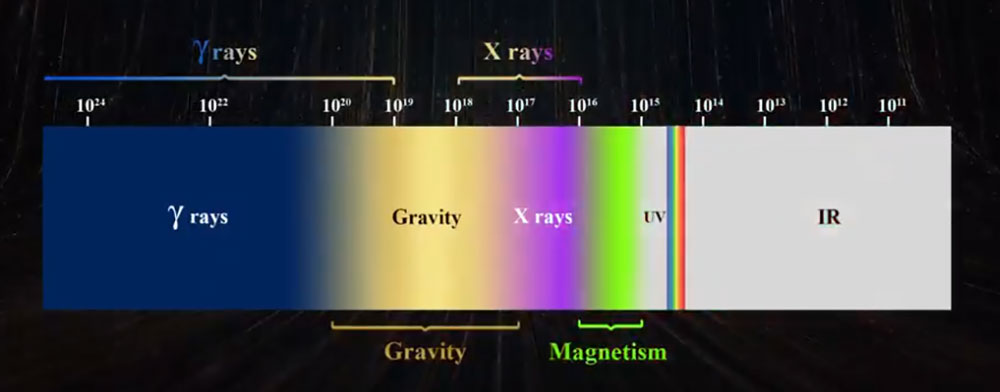
Fig. 1
2. New Explanation for the Intense Attraction and Repulsion of the Magnetic Poles
We should note that same as the electricity that electrons from higher potential points transfer to lower potential points, in magnetic fields also magnetic fluxes move from N pole by higher potential to the S pole.

Fig. 2
If magnetic poles be opposite, they will attract each other intensely and if the poles be alike, they repel each other intensely. Generally, it can be concluded that like poles repel each other with a force equal to the sum of the two values of those forces, and opposite poles attract each other with a force equal to the sum of the two values of those forces (Fig. 2):
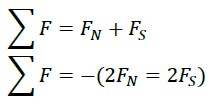
3. Nature and Structure of Magnetic Fluxes
According to relative penetrability of magnetic fields and its special and beautiful state, it can be said that magnetic waves are not single photons. Rather, they are a group of photons that are joined together in a chained state. For better conception it can be said whenever we bring two like poles of the magnet closer to each other, the contrary effect is seen, as if we have placed two invisible springs between them and we are squeezing the springs. These springs are the same as continuous magnetic fluxes.
Due to this special form, it can be said that the structure of the magnetic field is similar to the structure of gravity flux and chained photons. Since in this model, toward the linear direction, the fluxes are firm and steady and to the perpendicular direction, they have curvature property. These magnetic fluxes are made of photons, but the placement and structure of these photons are interconnected like chains. In fact, magnetic fluxes bend and compact and again return to their original shape. So it can be said that the magnetic field fluxes, similar to gravity fluxes, are made of interconnected like photons.




